hashtable前置知识
哈希表的基本概念、碰撞解决方法(线性探测、二次探测、复式散列、开链法)。
hashtable 前置知识
- 二叉搜索树(BST):平均时间复杂度是对数级
O(log n),但前提是假设输入数据有足够随机性。 - 红黑树(RB-tree):一种高效的平衡二叉搜索树,STL
set/map底层采用。 - hashtable(散列表):在插入、删除、查找等操作上,可以实现常数平均时间
O(1)的性能,并且不依赖数据随机性,而是基于统计特性。
hashtable 的本质
- 结构定义:可视作一种字典(dictionary),支持快速的“键-值”映射。
- 目标:在 常数时间 完成插入、删除、查找操作,类似于
stack或queue的操作效率。
理想化的直接寻址法
假设元素是 16 位无符号整数(范围 0~65535):
- 直接用一个长度为
65536的数组A,索引就是元素值。 - 操作方式:
- 插入元素 i:
A[i]++ - 删除元素 i:
A[i]-- - 查找元素 i:检查
A[i]是否为 0
- 插入元素 i:
- 特点:所有操作
O(1),简单直接。 - 缺点:
- 如果是 32 位整数,需要
2^32个数组槽位(约 4GB 空间),不现实。 - 如果元素类型是字符串等非整数类型,无法直接作为数组索引。
- 如果是 32 位整数,需要
直接寻址法的字符串改造(不实用)
- 将字符串映射为整数: 例
"jihou"→j*128^4 + i*128^3 + h*128^2 + o*128^1 + u*128^0 - 问题:映射值会非常大(例:
"jihou"对应28678174709),需要的数组规模依然过大。
引入 hash function(散列函数)
目的:将大范围的键映射为较小的整数索引(可接受的数组大小)。
例:
1
index = x % TableSize; // 结果范围在 [0, TableSize - 1]
好处:显著减少数组规模。
碰撞(collision)问题
- 不可避免:元素总数可能大于数组容量,不同元素会映射到同一索引。
- 解决方法:
- 线性探测(linear probing):依次向后查找空槽。
- 二次探测(quadratic probing):按平方距离跳跃查找。
- 开链法(separate chaining):每个槽位用链表存放多个元素。
- 不同方法效率不同,且与 装填因子(load factor) 密切相关。
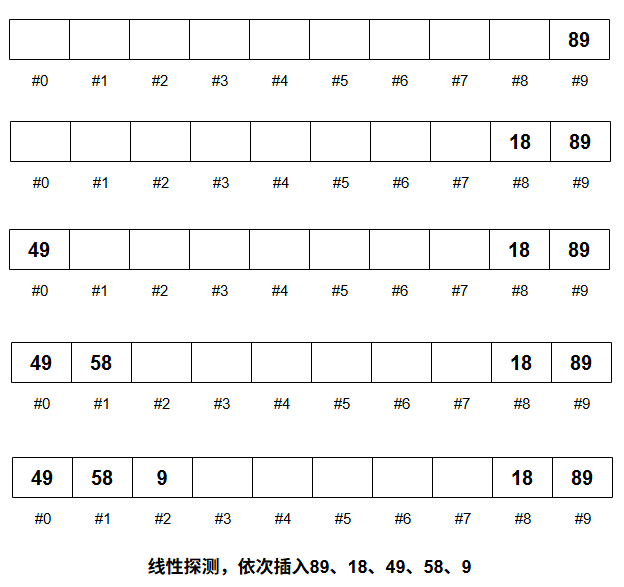
线性探测(Linear Probing)
负载系数(Loading Factor)
定义: \(\text{负载系数} = \frac{\text{元素个数}}{\text{表格大小}}\)
范围:
0 ~ 1(除非采用开链法,可以大于 1)。意义:衡量哈希表的“填满程度”,对性能有重要影响。
基本思想
- 当哈希函数计算出的插入位置已被占用:
- 顺序向后查找下一个位置(到表尾则回绕到表头)。
- 直到找到一个空槽(插入)或匹配元素(查找)。
- 删除策略:
- 采用 惰性删除(lazy deletion):标记已删除,但不立即清空元素。
- 原因:直接清空可能破坏其它元素的探测路径。真正删除在 rehashing 时进行。
时间复杂度分析
假设:
- 表格足够大。
- 元素的哈希值相互独立。
- 最坏情况:可能巡访整个表格,时间复杂度
O(n)。 - 平均情况:约巡访一半表格,仍然远大于理想的
O(1)。 - 实际情况往往更差,因为假设 2 不成立——这会导致元素聚集。
主集团(Primary Clustering)现象
- 线性探测的最大问题:会形成连续的一大段已占用的格子。
- 一旦形成主集团:
- 新元素容易落在集团的开头位置,被迫沿着集团探测。
- 插入过程会加大集团规模,使冲突进一步恶化。
- 结果:平均插入成本的增长速度远高于负载系数的增长速度。
示意图
- 已经连续占用了 0,1,2,8,9,它们连成一个大块(主集团)
- 只要新元素的哈希值落在 8、9、0、1、2 这一片范围,都会从它自己的哈希位置开始往后线性探测,最终依次占用 3、4、5、6、7 前的空位。
- 但如果哈希值落在 3、4、5、6、7,它会直接放到自己位置上,不用进入主集团往后线性探测。
小结
| 特性 | 说明 |
|---|---|
| 冲突处理方式 | 顺序探测下一个空槽 |
| 优点 | 实现简单,无额外指针开销 |
| 缺点 | 主集团效应严重,性能下降明显 |
| 删除方式 | 惰性删除,避免破坏探测链 |
| 适用场景 | 装填因子较低,数据分布较均匀时 |
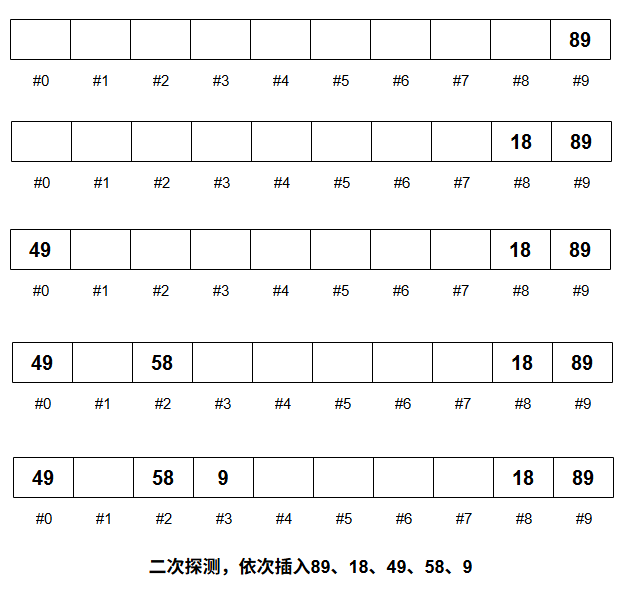
二次探测(quadratic probing)
二次探测(quadratic probing)是一种解决线性探测主集团(primary clustering)问题的方法。
具体做法是:
如果哈希位置 H 被占用,不是简单地往后一个一个找,而是按二次方增量探测,探测序列为: \(H, H + 1^2, H + 2^2, H + 3^2, \ldots, H + i^2\) 其中 $H$ 是初始哈希位置,$i$ 是探测次数。
这样探测的位置间隔会越来越大,避免了线性探测中连续聚集形成的主集团。
二次探测中的加减交替变体
- 纯二次探测:只用 $H + i^2$
- 加减交替探测:用 $H \pm i^2$,交替尝试两边位置
二次探测(quadratic probing)中,有一种常见的变体,会在探测序列里对平方步长加减交替使用,即探测序列类似于: \(H, H + 1^2, H - 1^2, H + 2^2, H - 2^2, H + 3^2, H - 3^2, \ldots\) 这样设计的目的是让探测更均匀地分布在哈希表的两侧,避免所有探测都往一个方向“挤”,进一步降低碰撞和主集团的风险。
具体使用哪种,取决于实现细节和哈希表大小,但加减交替版本确实更常见于实际应用中。
疑问与解答
- 二次探测是否能保证每次探测位置都不同? 以及如果表中没有元素X,是否一定能成功插入X?
- 如果哈希表大小是质数(prime),且负载因子保持在 0.5 以下(超过则扩容),则保证二次探测不会重复探测同一位置,且一定能找到空位插入新元素。
- 此条件下,插入新元素时的最大探测次数不超过 2 次,效率较高。
- 二次探测相比线性探测,计算复杂度是否太高,影响效率?
- 线性探测计算简单:只需加1及少量判断。
- 二次探测表面复杂,涉及平方和模运算,但可以通过递推优化避免乘法(例如通过前后探测位置差值递推计算),且乘法可以用位移优化。
- 这种优化使得二次探测的开销大幅降低,权衡来看,避免主集团带来的性能损失更值得。
- 负载因子过高时,是否支持动态扩容?
- 支持动态扩容,通常扩容时选择下一个较大的质数表大小(大约是当前的两倍),重新哈希所有元素到新表。
- 重建成本较高,但整体提升查询与插入效率。
其他说明
- 主集团(Primary Clustering):线性探测容易产生。
- 次集团(Secondary Clustering):二次探测减少主集团,但仍可能产生次集团——哈希值相同的元素探测序列相同,仍会浪费空间。
- 解决次集团的方法之一是复式散列(Double Hashing)。
复式散列(Double Hashing)
复式散列是一种解决哈希冲突的方法,属于开放地址法的一种。它通过使用两个不同的哈希函数来计算探测序列,从而减少主集团和次集团现象,提升哈希表的性能。
具体做法是:
初始哈希位置由第一个哈希函数计算得出: \(H_1(x) = h_1(x)\)
当发生冲突时,使用第二个哈希函数计算步长: \(H_2(x) = h_2(x)\)
探测序列为: \(H_i(x) = (H_1(x) + i \times H_2(x)) \bmod M\) 其中 $i = 0, 1, 2, \ldots$,$M$ 是哈希表大小。
这样,每次冲突探测的位置间隔由 $H_2(x)$ 决定,不是固定的步长,能更均匀地分布探测序列,避免线性或二次探测中产生的连续聚集问题。
开链法(Separate Chaining)
开链法(拉链法)是解决哈希冲突的另一种常用方法,与二次探测等开放地址法不同。其核心思想是:
- 哈希表的每个槽(桶)不仅存储单个元素,而是维护一个链表(list)或者其他结构。
- 元素经过哈希函数计算后,分配到对应的链表中。
- 插入、搜索、删除操作都在该链表中进行,链表的查找是线性的。
- 虽然链表查找是线性时间,但只要链表长度足够短,整体操作依然高效。
- 采用开链法时,负载因子可以大于1,因为多个元素可以存储在同一个槽的链表中。
SGI STL 的哈希表就是采用开链法实现。