RB-Tree前置知识

RB-Tree 前置知识

二叉搜索树

二叉树

二叉树（binary tree） 是一种每个节点最多有两个子节点的数据结构，分别称为左子节点和右子节点。可以用递归方式定义：一个非空二叉树由一个根节点和左右子树组成，左右子树本身也是二叉树，且可以为空。

二叉树用途广泛，例如表达式树、哈夫曼编码树等都属于二叉树。

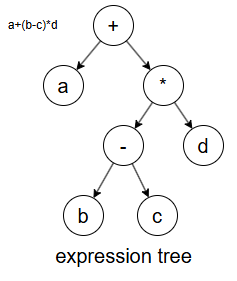
表达式树（Expression Tree）

• 用于表示算术表达式的二叉树。
• 叶子节点是操作数（数字或变量）。
• 非叶子节点是操作符（如 +、-、*、/）。
• 可以通过遍历表达式树来计算表达式值或生成表达式的不同形式（如中序、前序、后序表达式）。

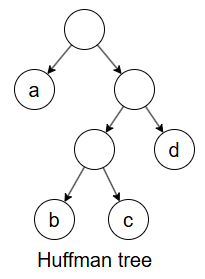
哈夫曼编码树（Huffman Coding Tree）

• 用于数据压缩的二叉树结构。
• 通过字符出现频率构造一棵最优二叉树，使得频率高的字符编码更短，频率低的字符编码更长。
• 树的叶子节点代表字符，路径上的左右分支对应编码的0和1。

二叉搜索树

二叉搜索树（Binary Search Tree） 是一种支持对数时间复杂度插入和查找的数据结构。其规则是：每个节点的键值大于左子树所有节点，小于右子树所有节点。

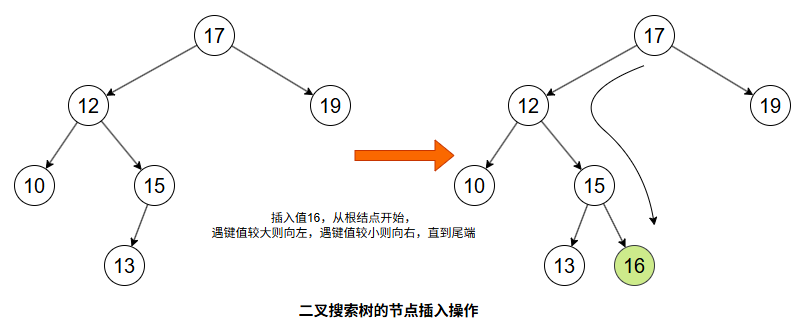
插入操作

1. 从根节点开始比较，若插入值小于当前节点，则进入左子树，否则进入右子树。
2. 递归或迭代地找到一个空位置，将新节点插入该处（作为叶子节点）。
3. 插入后，BST 的性质依然保持。

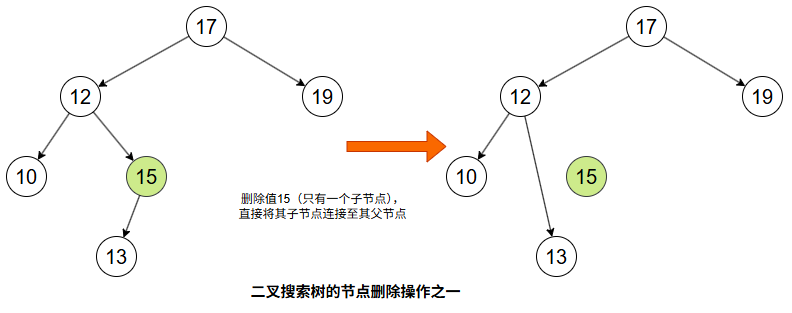
删除操作

删除节点 A 有三种情况：

1. A 是叶子节点：直接删除。
2. A 只有一个子节点：用 A 的子节点替代 A。
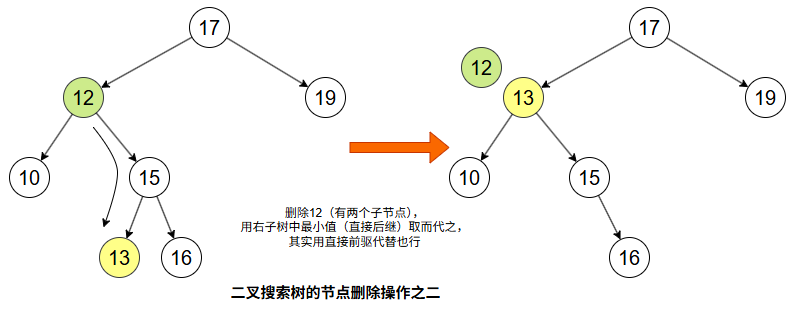
3. A 有两个子节点：找到 A 右子树中的最小节点（后继节点），用该节点的值替换 A 的值，然后删除后继节点（该节点最多只有一个右子节点），保持 BST 结构。

实际上，删除有两个子节点的节点时，既可以用右子树的最小节点（后继节点）替换，也可以用左子树的最大节点（前驱节点）替换，两者都是正确且常用的方法。

平衡二叉搜索树

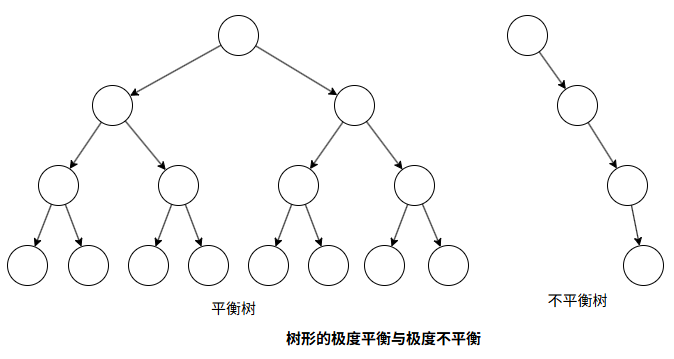
由于输入不够随机，或插入/删除操作不当，二叉搜索树可能会失去平衡，从而导致查找效率下降。

“平衡”指的是树中没有节点过深，不同的平衡条件影响效率和实现复杂度。像 AVL 树、红黑树（RB-tree）、AA 树等特殊结构能保持二叉搜索树的平衡，避免最坏情况下的高度不平衡。虽然插入和删除操作稍复杂，但能显著提升平均查找效率，一般能节省约 25% 的查找时间。

AA 树

AA 树是一种自平衡的二叉搜索树，属于红黑树的简化版本。它通过引入“层级”概念，严格限制树的结构，使得实现比传统红黑树更简单。AA 树主要特点包括：

• 每个节点都有一个“层级”（level）值，用于维护平衡。
• 所有左子节点的层级严格小于父节点，右子节点的层级要么等于父节点（表示红链接）要么小于父节点。
• 通过两种旋转操作——“skew”和“split”——保持树的平衡。
• 具有与红黑树相似的性能，插入和删除操作的平均时间复杂度为 O(log n)。

AA 树设计简洁，易于实现，常用于需要平衡树但想简化实现复杂度的场合。

AVL tree

AVL 是一种 自平衡二叉查找树（Self-Balancing Binary Search Tree），它得名于两位发明者 Adelson-Velsky 和 Landis，是最早提出的自平衡二叉查找树之一。

AVL树是一棵二叉查找树（BST），但每个节点的左右子树高度差（平衡因子）最多为1，即：

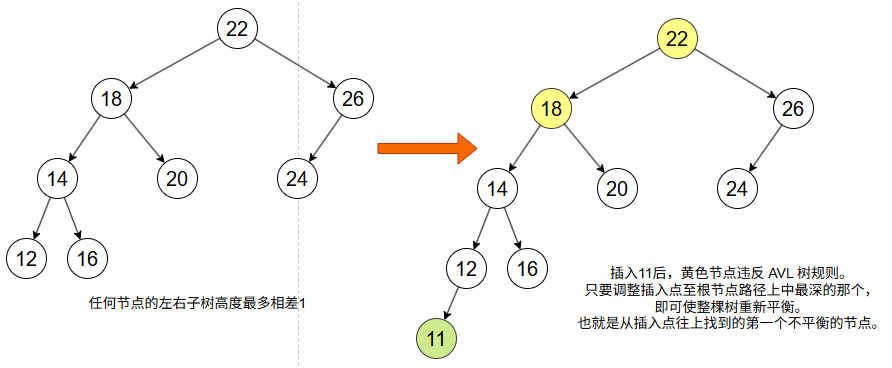
对于任意一个节点，|左子树高度 - 右子树高度| ≤ 1

这个条件保证了 AVL 树的查找、插入、删除操作的时间复杂度为 O(log n)。

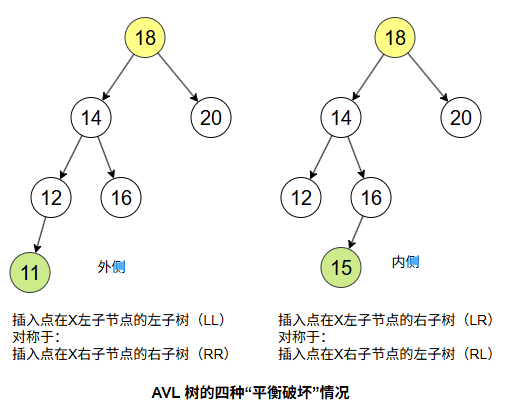
当插入破坏了AVL树的平衡时，只需调整路径上最深的失衡节点 X。失衡表现为 X 左右子树高度差为 2，分为四种情况：

失衡类型	修复方式	举例
左左（LL）	右旋（Right Rotation）	插入到左孩子的左子树
右右（RR）	左旋（Left Rotation）	插入到右孩子的右子树
左右（LR）	先左旋再右旋	插入到左孩子的右子树
右左（RL）	先右旋再左旋	插入到右孩子的左子树

外侧插入用单旋转修正，内侧插入用双旋转修正。

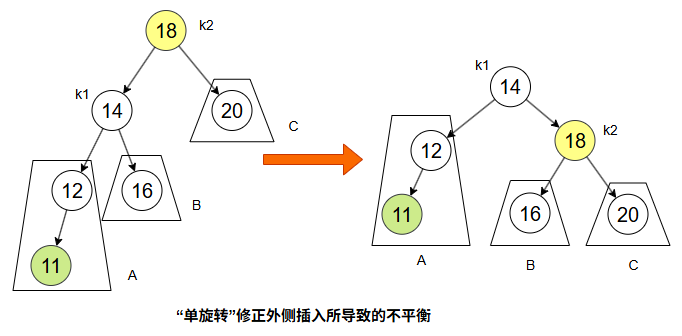
单旋转

外侧插入导致不平衡时，只有一种情况：左子树 A 增长了一层，使得其高度比右子树 C 多 2。

为了恢复平衡，我们将 A 子树上移一层，C 子树下移一层，即对失衡节点 k2 做一次右旋操作。旋转后，k1 变为根，k2 成为其右子节点，B 子树挂在 k2 的左侧，保持了二叉搜索树的顺序性质。这个调整只需移动指针，完成后树恢复平衡，无需额外操作。“右右”外侧插入的调整方法类似。

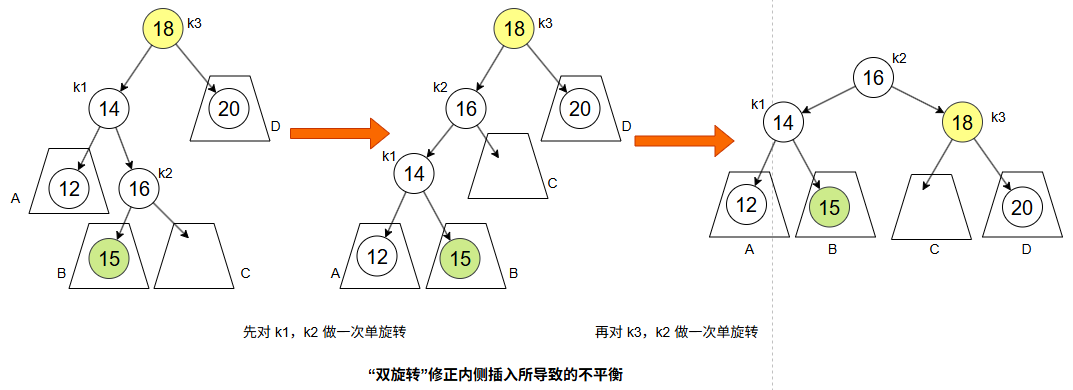
双旋转

内侧插入导致的不平衡无法通过单旋转解决，因为旋转后仍不平衡。正确的做法是以中间节点 k2 作为新的根节点，左子节点为 k1，右子节点为 k3，四个子树位置也随之确定。这种调整称为双旋转，实际上是两次单旋转的组合，能恢复平衡并保证树高度不变，无需继续调整。“右左”内侧插入的处理方法类似。

手动模拟旋转操作

不管单旋转还是双旋转，都是一样的操作流程：从插入的节点往上找到第一个不平衡的节点 X，然后从 X 往下，沿着刚才找上来的路径，从上往下选中最近的两个，加上 X 一共三个节点。把这三个节点构成一个最普通的二叉搜索树，一个根节点加左右孩子。这三个节点原来还有四棵子树（有可能是空树），把它们从左往右接在三个节点构成新的二叉搜索树的叶子节点上，如果是空树就跳过。最后把这个整理后的子树，接回原来 X 在整棵树中的位置。

与普通 BST 的比较

特性	普通 BST	AVL 树
查找效率	最坏可达 O(n)	保证 O(log n)
插入/删除效率	简单但可能退化	稍复杂但保持平衡
是否平衡	否	是（严格平衡）